算法分析 (一)- Analysis of Algorithm

算法分析 (一)- Analysis of Algorithm

---

算法分析是关于计算机程序性能和资源利用的研究,这是关于性能的课程

什么是比性能更重要呢?

• 可维护性
• 软件的健壮性
• 特性
• 功能化 - 可复用行
• 安全性
• 可拓展性
• 用户友好
• …

为什么还要关注性能?

• 一 、 性能的好坏 往往直接决定这可行性 【算法能够将不可行变成可行】
• 二 、 是一种描述性语言，是一种让程序最为简洁的思考方式，性能是确保良好的用户体验的前提，也是安全的保障。
• 三、带来喜悦，追求速度。

排序问题 - Problem Sorting

输入序列，输出有序的数列。

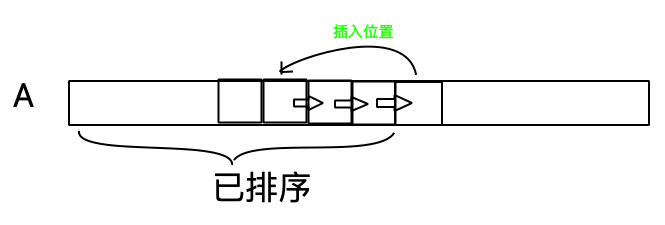
Sorting 1 - Insertion Sort

伪代码

InsertionSort(An) // Sorts A[1 ... n]
for i <- 2 to n
    key <- A[i]
    j <- i -1
    while j > 0 && A[j] > key
        A[j] <- A[j-1]
        j <- j-1
    A[j+1] <- key

示例

void InsertionSort(int [] n){
    for(i = 2; i < n.length() ; i++){
        int key = n[i];
        int j = i - 1;
        // 大元素后移
        while(j > 0 && n[j] > key){
            n[j+1] = n[j];
            j --;
        }
        // 插入位置 【j+1 -> 最后一次 循环 j 与插入位置 差 1】
        n[j+1] = key;
    }
}

运行时间

• 取决于输入的内容
• 取决于输入的大小
  • 依据输入的规模进行参数化
• 运行时间的上界 【该算法 至少运行 3秒？？？显然不合理】代表了对用户的承诺

对时间的分析方法

1. 最长运行时间
   • T(n) = max Time on any input of size
   • T(n)在某种意义上表示的是一种相关性，而不能算函数
   • 如果使用最大值就可以是函数关系， 因为运行的最大时间只有一个。

2. 平均运行时间

   • T(n) 就变成了所有输入的期望时间
   • 每种输入的运行时间 * 输入出现的概率值 【加权平均数】
   • 不可能知道每种输入的概率 - 所以需要作出假设，通常使用 均匀分布，即 每种输入出现的概率相同

3. 最好输入情况 (假象) - (下界 )

插入排序的最坏时间

依赖于计算机

• 同一个计算机运行不同的算法 - 对比的是相对时间
• 同一个算法运行在不同的计算机上，不一定都很快 - 对比的是绝对时间

BIG IDEA

针对以上两种情况 产生了 大局观(BIG IDEA)

即 渐进分析(asymptotic anaiysis)

思路

1. 忽略掉依赖于计算机的常量
2. 不是去检查运行的实际时间，而是关注运行时间的增长 T(n) n->∞

函数

1. θ 符号

   丢弃低阶项，并忽略常数因子

Ex: $3n^3 + 90n^2 - n = \theta(n^3)$

当 n ->∞ ， θ(n³) 迟早高于 θ(n²) 【与常数项是无关的 只不过交点x坐标的大小】 同时满足以上两种对比(未知)

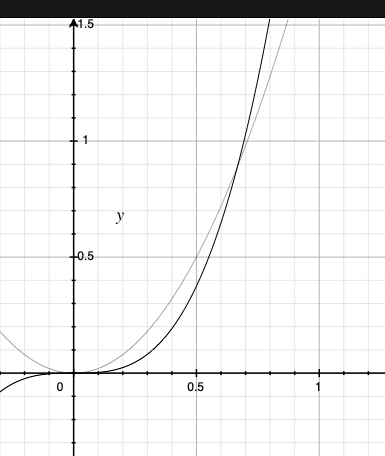
一开始，尽管 n² 在渐进的观点来看是慢的，但是仍可以在合理(数据量少)的输入下是快的。
因此需要在数学理解和工程直觉 上做好权衡才能写出更好的程序

最坏情况分析

• 输入顺序为 逆序

内存引用计数，某个变量访问的次数

1. $$T(n) =\sum_{i=2}^n\theta(i) = \theta(n^2)$$

$$θ(i) : 执行 i 次的时间$$ $$θ(n^2): 类似 1 + 2 ... + n = n(n+1)/2 = \theta(n^2)$$

• θ符号是一种弱符号运算。 极限的莱布尼茨 公式 是强符号运算。

所以 ： 插入排序的最坏时间 为 T(n²)

参考信息

学习视频